Cvičení 5 - Geometrické transformace
A) Teoretický úvod
Geometrické transformace se obecně řadí do kategorie předzpracování obrazu, kde mají za úkol korigovat geometrické distorze vzniklé při pořízení obrazu. Stoprocentní kategorizace ale není přesná, protože geometrické transformace je třeba použít i pro jiné úlohy např. rozpoznávání vzoru zejména při OCR. Formálně je geometrická transformace vektorová funkce T mapující polohu bodu se souřadnicemi (x,y) na nové souřadnice (x',y'). Pokud předpokládáme transformace v rovině, je matematicky vektorová funkce T složená ze dvou komponent Tx a Ty.
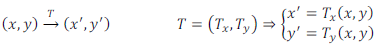
Tento předpis pro obecnou transformaci nedefinovaného stupně je zpravidla v praxi aproximován tzv. bilineární formou, v níž se vyskytují dvě čtveřice koeficientů popisujících geometrickou transformaci v rovině (v následujícím vztahu sloupec vlevo). Ještě dalšího zjednodušení lze dosáhnout vypuštěním součinového činitele xy a obdržet tak afinní formu geometrické transformace (sloupec vpravo).
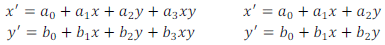
Výhodou afinní transformace je fakt, že přes svoji matematickou jednoduchost obsahuje čtyři základní geometrické transformace: translace, rotace, měřítko a zkosení. Každou z těchto čtyř základních transformací lze vyjádřit explicitně a následně je všechny maticovým násobením kombinovat do afinní formy kvůli výpočetní náročnosti. Poté už ale nelze z koeficientů ai a bi jednoznačně určit, jaká část řeší rotaci, jaká zkosení apod. Vztah pro translaci tj. posunutí obrazu je zjevně dán koeficienty a0 (posunutí ve směru x) a b0 (ve směru y). Měřítko určují koeficienty a1 a b2, zkosení a2 a b1.
Geometrická transformace pro otočení obrazu o libovolný úhel α proti směru chodu hodinových ručiček a kolem počátku souřadnicového systému využívá koeficienty {a1,a2} a {b1,b2} a je explicitně dána následujícím vzorcem.
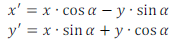
Použitím goniometrických funkcí je zřejmé, že na pevně daném digitálním rastru dojde při takovéto transformaci k chybám daným neceločíselnými výsledky souřadnic ve výstupním obrazu. V přesných výpočtech se tyto chyby minimalizují interpolací jasových hodnot anebo méně přesně prostým zaokrouhlením.
Geometrické transformace se někdy využívají také jako součást výpočtu složitějších operací. Příkladem jsou integrální transformace a konkrétně Radonova transformace, která je zobecněním známější Houghovy transformace používané pro detekci geometrických entit zejména přímek a křivek nízkých řádů. Radonova transformace integruje obrazovou funkci f(x,y) přes přímky pomocí jediného parametru α, který udává míru otočení obrazu před samotnou integrací. Formálně je spojitá Radonova transformace definována jako integrál funkčních hodnot podél parametricky určené přímky a je dána následujícím vztahem.
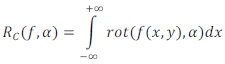
Diskrétní formulaci přímé Radonovy transformace s parametrem α lze chápat jako vektor součtů jasových hodnot podél řádků obrazu otočeného o úhel α, tedy podle vzorce pro R(f,α).
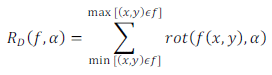
Je zřejmé, že přímou Radonovu transformaci lze využít pro detekci čárových úseků v obrazu jeho postupným otáčením a integrací řádků nebo přímo integrací podél vypočtených souřadnic přímky. Poskládáním vektorových odezev přímé Radonovy transformace vedle sebe vznikne obraz podobný akumulátoru Houghovy transformace, v němž lze snadno detekovat globální a lokální extrémy a určit tak čárové úseky v obrazu. Opačná varianta tedy inverzní Radonova transformace (využívající formy Fouriérovy transformace) není předmětem cvičení a používá se výhradně pro rekonstrukci obrazů počítačové tomografie.
B) Úkoly
- Napište funkci [J] = AffineTransform(I,a,b), která nad obrazem I provede afinní transformaci podle koeficientů předaných v parametrech a a b (tříprvkové vektory) a výsledek uloží do obrazu J (stejné velikosti jako I). Pomocí této funkce a vhodně zvolených koeficientů proveďte translaci, změnu měřítka a zkosení obrazu obraz07.bmp.
- Určete, kolik je třeba znát vzájemně korespondujících si bodů ve vstupním a výstupním obrazu, aby bylo možné jednoznačně určit matematický předpis neznámé afinní transformace.
- Napište funkci [J] = ImageRotate(I,α) pro natočení vstupního obrazu I o úhel α se středem otáčení uprostřed obrazu. Výstupní obraz J musí mít stejné rozměry jako obraz vstupní a obsahovat jeho střední část, tj. chybějící body doplňte nulou a přesahy ořežte. Správnost implementace ověřte na obraze lenaM.bmp
- Implementujte funkci [R] = ImageRadon(I) realizující Radonovu transformaci vstupního obrazu I. Pomocí této funkce sestavte algoritmus pro výpočet úhlu natočení dominantních čar v obrazu a ověřte jej na dvou obrazech pruhy_diag.bmp a obraz07.bmp. Výslednou dominantní čáru zobrazte v originálním snímku pomocí funkce line a do titulku obrazu vepište hodnotu změřeného úhlu.
C) Dobré vědět
- Povolené funkce: sin, cos
- Nepovolené funkce: imtransform, imrotate, radon
D) Ilustrace výsledků